Python からはじめる数学入門 (Doing Math with Python)(まとめ記事)の第 6 章を読む。第 2 章「Visualizing Data with Graphs( まとめ記事)」の続編という感じで、幾何学図形やアニメーションなど matplotlib の別の機能を試す。後半は フラクタル の摩訶不思議な世界を垣間見る。matplotlib の新たな機能 imshow() を使いながら有名なマンデルブロ集合を描画したり、章末問題も好奇心をくすぐる内容で見逃せない。
内容
- matplotlib
FigureクラスとAxesクラス- しかし相変わらず MATLAB 形式で書かれているのが残念
- → 自分でオブジェクト指向形式に変更
- matplotlib.patches モジュール: 図形
- matplotlib.patches.Circle クラス: 円
- matplotlib.animation モジュール: アニメーション
- matplotlib.animation.FuncAnimation クラス
- 実例: 放物運動
- フラクタル
- Barnsley Fern(バーンズリーのシダ)
ポイント
注意が必要な点や、感銘を受けた内容について。
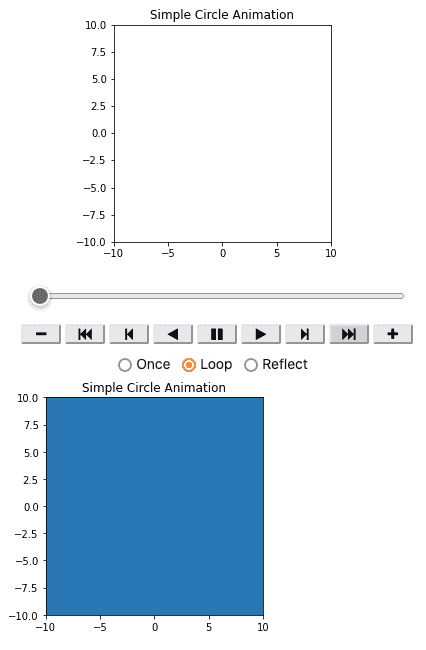
matplotlib のアニメーションを JupyterLab で表示
デフォルトでは JupyterLab でアニメーションが表示されない。JupyterLab 上で matplotlib のアニメーションを出力する - Qiita によると、 IPython.display.HTML を利用する方法が一番簡単なようだ。
import matplotlib.animation as animation
import matplotlib.pyplot as plt
from IPython.display import HTML
fig, ax = plt.subplots()
# 省略
# アニメーションを作成
anim = animation.FuncAnimation(
fig, update_radius, fargs=(circle,), frames=30, interval=50
)
# 下に不要なグラフが表示されるのを避ける
plt.close()
# アニメーションをHTML形式で表示
HTML(anim.to_jshtml())インタラクティブなナビゲーション・メニュー付きでアニメーションが表示できる。
ただし、上のスクリーンショットのように下に 不要なグラフが表示 されてしまうので、それを避けるために plt.close() を(最後から 2 番目に)追加する。
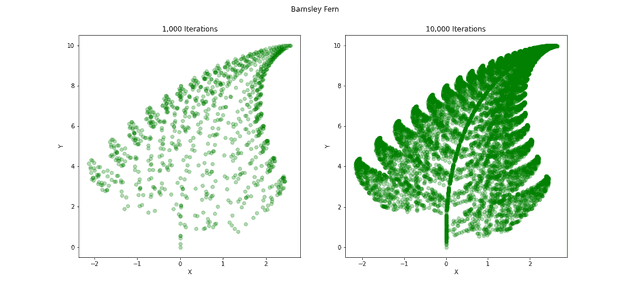
Barnsley Fern(バーンズリーのシダ)
Barnsley Fern(バーンズリーのシダ)は、原点から開始して、特定の発生確率 でランダムに 4 種類のアフィン変換 を繰り返した軌跡として描かれる図形。
def transform(p):
# List of transformation functions
transformations = [
transformation_1,
transformation_2,
transformation_3,
transformation_4,
]
# Pick a random transformation function and call it
t = random.choices(transformations, weights=[85, 7, 7, 1])
return t[0](p)アフィン変換のランダムな選択には、標準ライブラリの random.choices 関数を利用してみた。
確かにシダ植物に似ている。シンプルな規則から、自然界に潜む自己相似性が生まれる様子は、非常に興味深い。
プログラミング・チャレンジ(章末問題)
- #1: Packing Circles into a Square
- パッキング問題(四角形に円を出来る限り詰め込む)の簡易版
- → Jupyter ノートブック
- #2: Drawing the Sierpiński Triangle
- シェルピンスキーの三角形 を描く
- → Jupyter ノートブック
- #3: Exploring Hénon’s Function
- エノン・アトラクタ を描く
- → Jupyter ノートブック
- #4: Drawing the Mandelbrot Set
- matplotlib.axes.Axes.imshow() メソッドを利用して画像を表示
- マンデルブロ集合 を描く
- → Jupyter ノートブック
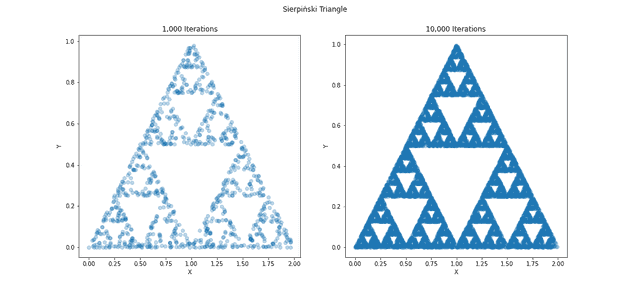
#2: Drawing the Sierpiński Triangle
三角形から等分の三角形を無限に抜くことを繰り返して描けるシェルピンスキーの三角形だが、これもバーンズリーのシダと同じように、3 種類のアフィン変換をランダムに繰り返す事でも得られるらしい。
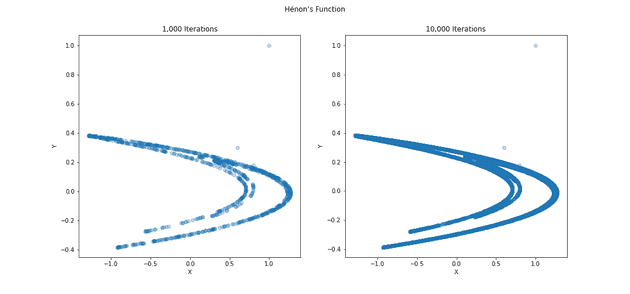
#3: Exploring Hénon’s Function
エノン写像 とは、2 変数連立常差分方程式(漸化式)で定義され、2 次元の離散力学系の一種らしい。今回描く エノン・アトラクタ とは、エノン写像に特定のパラメータを与えた時に得られる曲線。
動画で見ると、曲線は連続的ではなく、バラバラに描かれる様子が観察できる。
https://www.youtube.com/watch?v=76ll818RlpQ
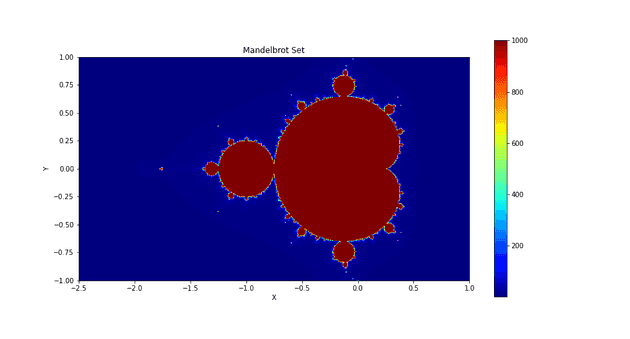
#4: Drawing the Mandelbrot Set
複素平面上の任意の点 に対して、次のような漸化式で定義される複素数列 を考える。この数列が発散しない点 全体が作る集合をマンデルブロ集合と呼ぶ。
計算機上では簡易的に、1,000 をループ回数の上限として、数列の絶対値 が 2 を超えるループ回数 を計算する。複素平面の任意の点に対して、その ループ回数ごとに色分け することで図形を描く。発散するまでの回数を評価するという意味で、Escape-Time Algorithm とも呼ばれるらしい。
def escape_time(x, y):
# Maximum iterations
max_iteration = 1000
c = complex(x, y)
z = complex(0, 0)
iteration = 0
while abs(z) < 2 and iteration < max_iteration:
z = z ** 2 + c
iteration += 1
return iterationこの出力で色分けすると、有名なパターンが現れる。
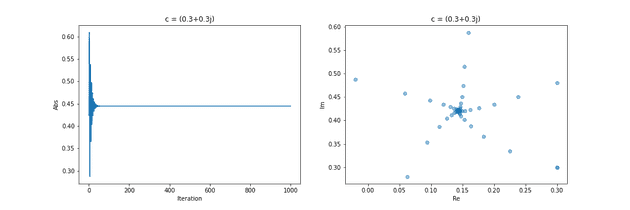
折角なので、幾つかの点に対して発散の様子を観察してみる。まずは発散しない の場合から。左側のグラフは横軸がループ回数、縦軸が数列の絶対値を表す。右側のグラフは散布図を複素平面に見立てて、数列の各項をプロットしたもの。数列はヒトデのような形を描きながら、一点に収束しているように見える。
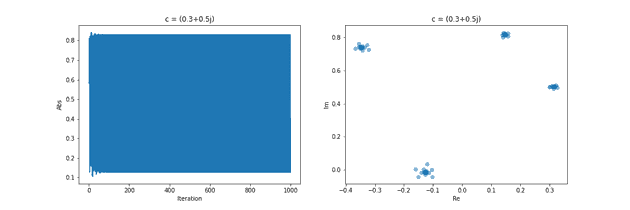
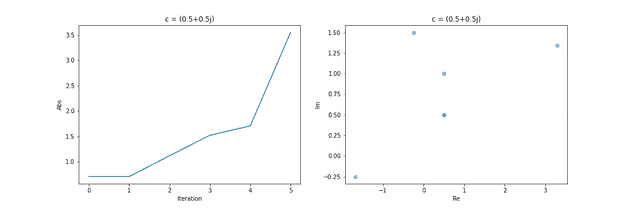
一方 では、数列は無限大には発散しないが、とびとびの 4 つのグループを形成しながら振動を続ける。
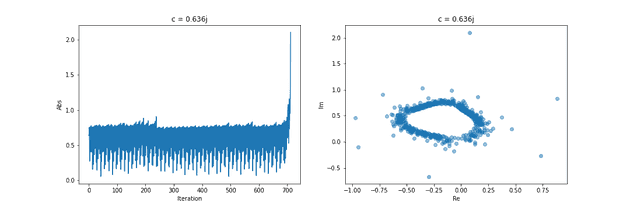
では、輪っかのような図形を描きながら振動した後に、ループ回数 700 を超えたあたりで最終的に発散している。恐らく マンデルブロ集合の縁 にあたる点と考えられる。
最後に では、ループ回数 5 程度であっさりと絶対値が 2 を超える。
このように、たった 4 つの点を観察するだけでも、フラクタルの複雑さを垣間見ることができた。
Chapter 7 のまとめ「Python からはじめる数学入門 - Chapter 7: Solving Calculus Problems を読む)」を公開しました!第 4 章に引き続き SymPy を使って、微分積分学の初歩に取り組みます。勾配降下法による関数の極値の計算など、応用も充実しています。