Pythonからはじめる数学入門 - Chapter 5: Playing with Sets and Probability を読む

Python からはじめる数学入門 (Doing Math with Python)（まとめ記事）の第 5 章を読む。テーマは 確率と乱数。準備として SymPy による集合を取り扱いを練習した上で、幾つか確率の計算をしてみる。乱数を用いた実験も行う。章末問題も面白い。

内容

  • sympy.FiniteSet: 有限集合
    • 定義（生成）: 要素の型はバラバラでも大丈夫
      • 空集合
      • リストやタプルから生成 → *（アンパック）が有効
    • len() 関数: cardinality（濃度）
    • 包含関係
      • in 演算子
      • is_subset() メソッド: 部分集合
      • is_proper_subset() メソッド: 真部分集合
      • is_superset() メソッド: スーパーセット
    • 集合演算
      • union() メソッド: 和集合
      • intersect() メソッド: 共通部分
      • * 演算子: 直積
      • ** 演算子: 直積の冪乗
      • powerset() メソッド: 冪集合
  • 確率
    • Experiment（試行）: サイコロを振る、コイン投げ など
    • Sample Space（標本空間）: サイコロの目、コインの表裏 など
    • Event（事象）: 偶数の目、コインの表 など
    • Uniform Distribution（一様分布）における確率の計算
    • 和事象
    • 積事象
  • random モジュール: 乱数生成
    • randint() 関数: 離散的な乱数
    • rand() 関数: 連続的な乱数
    • 非一様乱数
      • → Probability Number Line を 不等分 に分割

→ Jupyter ノートブック

プログラミング・チャレンジ（章末問題）

今回はやり甲斐があった！

#1: Using Venn Diagrams to Visualize Relationships Between Sets

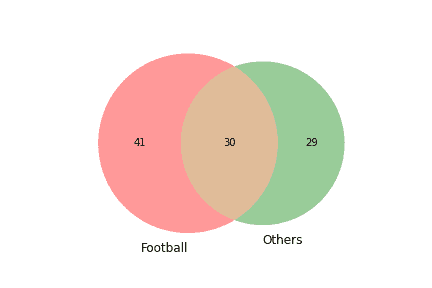
課題は、20 人の学生を対象としたアンケート結果（フットボールをやるか、他のスポーツをやるか）を CSV で読み取って、ベン図を描く。

しかし、それだけじゃ面白くないので、乱数でアンケート結果を生成してみる。

次のようにして、値が 2/32/3 未満ではフットボールをやる、1/31/3 より大きいときそれ以外のスポーツもやるとグループ分けする。random() 関数は一様乱数なので、3 グループが均等になるはず。

import random

import matplotlib.pyplot as plt
from matplotlib_venn import venn2

football = set()
others = set()

# generate random datas of 100 students
for i in range(100):
    r = random.random()
    if r < 2 / 3:
        football.add(i)
    if r > 1 / 3:
        others.add(i)

# draw a venn diagram
fig, ax = plt.subplots()
venn2(subsets=[football, others], set_labels=("Football", "Others"), ax=ax)
fig.savefig("chap5_pc1_using-venn-diagrams.png")
plt.show()

サンプルが少ないので残念ながら均等とは言えないが、だいたい分散してるようには見える。

Venn Diagram

#2: Law of Large Numbers（大数の法則）

サイコロを振る回数を徐々に増やして、出る目の平均値が期待値に近づくことを確かめる。

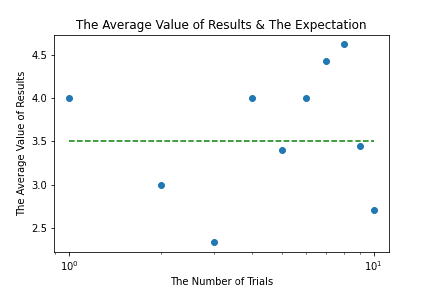
まずは 10 回まで。期待値 3.5 には程遠い。

Law of Large numbers (-10 Times)

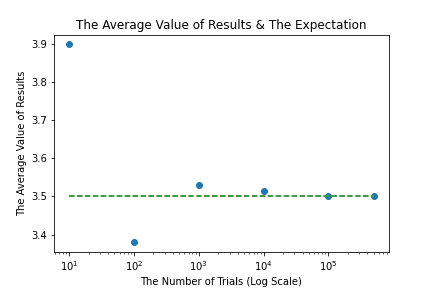
次に 10 回〜500,000 回まで。横軸は対数軸になっている。徐々に期待値 3.5 には近づいている事が確認できる。特に 10,000 回以降の差は特に小さい。

Trials: 10 Trial average 3.90000 (Difference: 0.40000)
Trials: 100 Trial average 3.38000 (Difference: -0.12000)
Trials: 1,000 Trial average 3.53000 (Difference: 0.03000)
Trials: 10,000 Trial average 3.51420 (Difference: 0.01420)
Trials: 100,000 Trial average 3.50258 (Difference: 0.00258)
Trials: 500,000 Trial average 3.50176 (Difference: 0.00176)

Law of Large numbers (10-500k Times)

#4: Shuffling a Deck of Cards

標準ライブラリの random.shuffle() 関数も使えるが、折角なので練習がてらに ダステンフェルドのアルゴリズム を実装してみる。

def shuffle(list):
    for i in range(len(list) - 1, 0, -1):
        j = random.randint(0, i)

        if i != j:
            # swap i-th & j-th items
            list[i], list[j] = list[j], list[i]


x = list(range(1, 10))
shuffle(x)
x
→ [9, 2, 8, 1, 7, 3, 4, 6, 5]

参考リンク フィッシャー–イェーツのシャッフル - Wikipedia

#5: Estimating the Area of a Circle

モンテカルロ法を利用して、円の面積（円周率）を計算する。

generate_darts() 関数は、沢山の点をランダムに生成して、円の内部と円の外部に分けて 点のリストを出力する。

def generate_darts(num_of_darts):
    inside_x = []
    inside_y = []
    outside_x = []
    outside_y = []

    for _ in range(num_of_darts):
        x = random.uniform(-1, 1)
        y = random.uniform(-1, 1)

        if check_inside_circle(x, y):
            inside_x.append(x)
            inside_y.append(y)
        else:
            outside_x.append(x)
            outside_y.append(y)

    return ((inside_x, inside_y), (outside_x, outside_y))

他には、点が円の内部かどうかを判定する check_inside_circle() 関数と、円の内部と外部で色分けして図にする drew_circle() 関数も定義する。

次のようにして、10310^3 から 10610^6 まで点の個数を増加させて、見積もり精度を評価してみる。

fig, ax = plt.subplots(2, 2, figsize=(12, 12))
ax = ax.flatten()


for i, num_of_darts in enumerate([1000, 10_000, 100_000, 1_000_000]):
    inside, outside = generate_darts(num_of_darts)

    estimation = len(inside[0]) / num_of_darts * 4
    print(
        "Area ({0:,} Darts): {1:.5f} ({2:.5f} %)".format(
            num_of_darts, estimation, (estimation - math.pi) / math.pi
        )
    )

    drew_circle(ax[i], num_of_darts, inside, outside)

fig.savefig("chap5_pc5_estimating-the-area-of-a-circle.png")
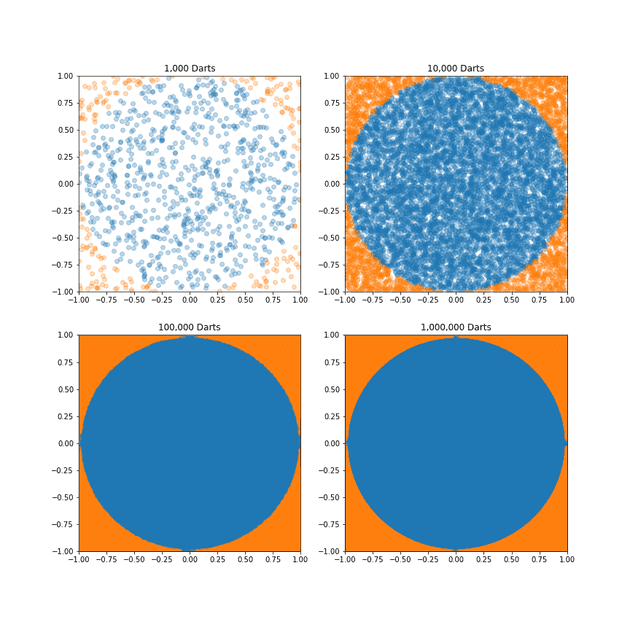
plt.show()

結果は次の通り。点の数が増えるに従い、精度が向上している事が確認できる。

Area (1,000 Darts): 3.18800 (0.01477 %)
Area (10,000 Darts): 3.15640 (0.00471 %)
Area (100,000 Darts): 3.14660 (0.00159 %)
Area (1,000,000 Darts): 3.14180 (0.00006 %)

図を見ると 100,000 以上（下段）では、ほぼきれいに塗りつぶされた円に見える。100,000（左下）と比べると、1,000,000（右下）は円周が、更に滑らかになっている。

Estimating the Area of a Circle

モンテカルロ法 - Wikipedia

Chapter 6 のまとめ「Python からはじめる数学入門 - Chapter 6: Drawing Geometric Shapes and Fractals を読む）」を公開しました！第 2 章「Visualizing Data with Graphs（ まとめ記事）」の続編という感じで、幾何学図形やアニメーションなど matplotlib の別の機能を試して行きます。後半は様々な フラクタル の、摩訶不思議な世界を覗きます。