Pythonからはじめる数学入門 - Chapter 4: Algebra and Symbolic Math with SymPy を読む

2021-12-23Python cas SymPy

Python からはじめる数学入門 (Doing Math with Python)（まとめ記事）の第 4 章を読む。コンピュータ代数（数式処理） のパッケージ SymPy を利用して、数式を展開・因数分解したり、方程式を代数的に解いたりしながら、これまでの数値計算とは一味違った世界を垣間見る。

内容

Symbols（記号、数学的な意味での変数）の定義
Mathematical Expressions（数式）の定義
式変形
- factor() 関数: 因数分解
- expand() 関数: 展開
- simplify() 関数: 全自動の簡約化 ← 全能ではない！
- subs() メソッド: 式への置換（代入）
  - 数値を代入
  - 式を代入
式の表示
- pprint() 関数: 数式をアスキーアートで出力
- init_printing() 関数: 式の出力設定（項の表示順など）
  - 項を次数の昇順に並べたいが、order="grevlex" を指定しても思うように変化しない！
simplify() 関数: 文字列を式に変換（にも使える）
- 無効な文字列を与えた時は、例外 SympifyError が発生
solve() 関数: 方程式を解く
- 2 次方程式
  - 係数が数値の場合
  - 係数も記号（変数）の場合（一般的に解く）
- 2 元 1 次連立方程式
plot() 関数: グラフを描く
- 変数 $x, y$ の 2 元方程式のグラフ
  - $y$ について解いてから、plot() 関数に渡す
- 複数の関数のグラフ

→ Jupyter ノートブック

ポイント

本章を読んで気になったり、感銘を受けた内容について。

式の表示

JupyterLab で SymPy を使う場合は、SymPy の数式が自動的に $\LaTeX$ で美しく表示されるので素晴らしい！！

しかし従来の表示方法も一応確認しておく。

print() 関数: Python コードで表示
sympy.pprint() 関数: アスキーアート

例えば積分

$\int \sqrt{\frac{1}{x}}\, dx$

を考える。

expr = sympy.Integral(sympy.sqrt(1 / x), x)

print(expr)
→ Integral(sqrt(1/x), x)

sympy.pprint(expr)
⌠
⎮     ___
⎮    ╱ 1
⎮   ╱  ─  dx
⎮ ╲╱   x
⌡

項の表示順

数式は高次の項から降順に自動的に並び替えて表示される。

expr = 1 + x + 2 * x ** 2
expr

→ $2 x^2 + x + 1$

init_printing() 関数に order="grevlex" を渡せば昇順で表示されるようになるはずだが、何故か思うように変化しない！

sympy.init_printing(order="grevlex")
expr = 1 + x + 2 * x ** 2
expr

→ $2x^2 + x + 1$

https://docs.sympy.org/latest/modules/interactive.html?highlight=init_printing#sympy.interactive.printing.init_printing

ちなみにテイラー展開をする series() メソッドを使うと、ちゃんと昇順に並ぶので何か正しい方法はあるはず。

expr = sympy.exp(x)
expr.series(x, 0, 5)

$1 + x + \frac{x^{2}}{2} + \frac{x^{3}}{6} + \frac{x^{4}}{24} + O\left(x^{5}\right)$

$\LaTeX$ コマンドで表示

latex() 関数を利用すると、SymPy の式が $\LaTeX$ コマンドに変換できる。コピペすると便利！！

expr = sympy.Integral(sympy.sqrt(1 / x), x)
print(sympy.latex(expr))
→ \int \sqrt{\frac{1}{x}}\, dx

有理数 `Rational`

Solving for One Variable in Terms of Others の運動方程式を解いていて気がついたのだが、本文にあるように (1 / 2) * x と書くと、 $0.5x$ と小数になってしまう。

SymPy には有理数を表す sympy.Rational クラスがあるので、それを利用して sympy.Rational(1, 2) * x と書くと良い。

https://docs.sympy.org/latest/modules/core.html#rational

プログラミング・チャレンジ（章末問題）

~~#1: Factor Finder~~ → スキップ
- ユーザ入力を受けて数式を因数分解する
#2: Graphical Equation Solver
- ユーザ入力（2 つの 2 元 1 次方程式）を受けて、グラフ表示して、方程式を解く
- → Jupyter ノートブック
#3: Summing a Series
- ユーザ入力（数列の一般項）を受けて、数列の和を計算する
- $\sum$ に相当する sympy.summation() 関数を利用
- → Jupyter ノートブック
#4: Solving Single-Variable Inequalities
- ユーザ入力（1 変数の不等号式）を受けて、不等号を解く
- → Jupyter ノートブック

#3: Summing a Series

一般項を渡すと級数の和を計算してくれる sympy.summation() 関数を利用する。試しに自然対数の底 $e = 2.71828182845905$ を計算してみる。一般項は次のように書ける。

term = 1 / sympy.factorial(n)

第 5 項まで計算する。小数点第 2 位まで一致する。

sum = sympy.summation(term, (n, 0, 5))
sum.evalf()
→ 2.71666666666667

次に第 10 項まで計算する。小数点第 7 位まで一致する。

sum = sympy.summation(term, (n, 0, 10))
sum.evalf()
→ 2.71828180114638

結構収束が速い事がわかる。

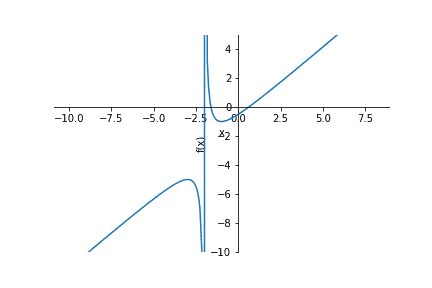
#4: Solving Single-Variable Inequalities

SymPy では、1 変数の不等号を解くができるが、式の種類によってソルバー関数が 3 種類に分かれる。

solve_poly_inequality(): 多項式
solve_rational_inequalities(): 有理式
solve_univariate_inequality: それ以外

それは良いが、途中で式を poly（多項式）に変換が必要だったり、有理式だけ [[ ... ]] で式を渡す必要があったりと、ちょっと使いにくい気がする。

# 解きたい不等式（有理式）
ineq_obj = ((x ** 2 + x - 1) / (x + 2)) > 0
# 分母と分子に分ける
numer, denom = ineq_obj.lhs.as_numer_denom()
# 分母と分子を Poly（多項式）へ変換
p1 = sympy.Poly(numer)
p2 = sympy.Poly(denom)
# 不等号を取得
rel = ineq_obj.rel_op
# 不等号を解く
sympy.solve_rational_inequalities([[((p1, p2), rel)]])

→ $\left(-2, - \frac{\sqrt{5}}{2} - \frac{1}{2}\right) \cup \left(- \frac{1}{2} + \frac{\sqrt{5}}{2}, \infty\right)$

ちゃんと代数的に解けている。グラフはこんなかんじ。

参考リンク

Sympy+Jupyter で最強の電卓環境を作る - Qiita

SymPy：計算機代数システム ←Python 数値計算入門の一部

入力例で学ぶ Python (SymPy) の使い方（入門） - pianofisica

Chapter 5 のまとめ「Python からはじめる数学入門 - Chapter 5: Playing with Sets and Probability を読む）」を公開しました！テーマは 確率と乱数。準備として SymPy で集合を取り扱った上で、幾つかの確率計算と、乱数を用いた実験を行います。