Pythonからはじめる数学入門 - Chapter 3: Describing Data with Statistics を読む

Python からはじめる数学入門 (Doing Math with Python)（まとめ記事）の第 3 章を読む。平均値・分散・相関係数など 記述統計学の入門編 と言える内容で、それらを Python の標準ライブラリだけ用いて計算する。また matplotlib を利用して散布図を描いたりもする。

内容

• Mean（平均値）
• Median（中央値）
• Mode（最頻値）
• Frequency Table（度数分布表）
• Variance（分散）
• Standard Deviation（標準偏差）
• Correlation Coefficient（相関係数）
• Scatter Plots（散布図）
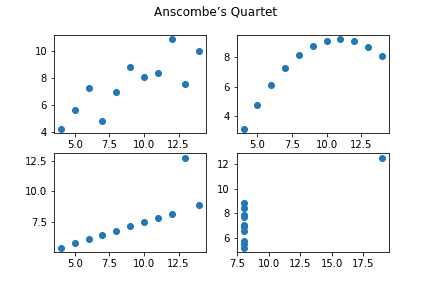
  • 例えば Anscombe’s Quartet の 4 つのデータセットは、平均値と標準偏差、相関係数がそれぞれ等しいにもかかわらず、散布図で見てみると様子が全く異なる。
  • → 可視化は大切！！外れ値の影響は気をつけよう！
• ファイルからデータの読み込み

→ Jupyter ノートブック

ポイント

本章を読んで気になったり、感銘を受けた内容について。

整数の割り算 //

本文では中央値を計算するのに、N/2（N: データのサイズ）を int() で整数に直してるけど、N//2 とすれば一発だと思う。

def calculate_median(numbers):
    N = len(numbers)
    numbers.sort()

    m = N // 2

    if N % 2 == 0:
        median = sum(numbers[m - 1 : m + 1]) / 2
    else:
        median = numbers[m]

    return median

collections.Counter

標準ライブラリの collections.Counter オブジェクトは、各要素の出現回数をカウントする機能を持つ。

c = Counter("hello")
type(c)
→ collections.Counter

キーにアルファベット、アルファベットの出現頻度を値に持つ、辞書と言える。

c
→ Counter({'h': 1, 'e': 1, 'l': 2, 'o': 1})

most_common() メソッドで、頻度順に並べたリストが得られる。

c.most_common()
→ [('l', 2), ('h', 1), ('e', 1), ('o', 1)]

elements() メソッドを利用すると、逆に Counter は希望する出現頻度のリストを生成するのに使える。

list(Counter({"a": 1, "b": 2, "c": 3}).elements())
→ ['a', 'b', 'b', 'c', 'c', 'c']

https://docs.python.org/ja/3/library/collections.html#collections.Counter

リストの内包表記

本文では最頻値や分散の計算など、いたるところで手続き型でリストの append() メソッドを多用している。しかし折角 Python で書くなら、内包表記を利用しないのはもったいないと思う。

例えば最頻値だと、手続き型では次のようになる。

modes = []
for num in numbers_freq:
    if num[1] == max_count:
        modes.append(num[0])
return modes

これが内包表記を一行で済む。

return [i[0] for i in numbers_freq if i[1] == max_count]

https://docs.python.org/ja/3/tutorial/datastructures.html#list-comprehensions

プログラミング・チャレンジ（章末問題）

• #1: Better Correlation Coefficient–Finding Program
  • 相関係数を計算する関数 find_corr_x_y() で、引数の長さが等しいか最初に確認する
  • → Jupyter ノートブック
• #2: Statistics Calculator
  • mydata.txt から統計量を計算する
  • → Jupyter ノートブック
• #3: Experiment with Other CSV Data
  • アメリカの人口増加の統計量を計算・可視化する
  • → Jupyter ノートブック
• #4: Finding the Percentile
  • パーセンタイルを計算する
  • → Jupyter ノートブック
• #5: Creating a Grouped Frequency Table
  • 階級ごとにグループ分けした度数分布表を作成する
  • → Jupyter ノートブック

#4: Finding the Percentile

パーセンタイルと言えば、4-2. 四分位数を見てみよう | 統計学の時間 | 統計 WEB のように、対応する値をそのまま取るか、前後 2 つの値の平均を取る方法しか知らなかったが、他にも色々なパーセンタイルの計算方法があるらしい。

1. データを昇順に並び替える
2. $i = \frac{np}{100} + 0.5$ （n はデータのサイズ）を計算
3. もし $i$ が整数の場合、$i$ 番目のデータが $p$ パーセンタイル
4. もし $i$ が整数でない場合、$k$ を $i$ の整数部、$f$ を小数部とする。(1-f)*data[k] + f*data[k+1] が $p$ パーセンタイル

ただし、ここでデータの インデックスは 1 から始まる ことに注意！！

ところで、2 番目の式に現れる $0.5$ とは何だろう？

答えは、50 パーセンタイルの時に上手く中央値を指すように調整するためだ。サイズが奇数の場合、例えば 7 個を考えたとき、$i = 3.5 + 0.5 = 4$ となって、確かに中央値と一致する。

3 番目の式についても、具体的に考えてみる。ここでは $a := \frac{np}{100}$ と置くことにする。

• $a = 3.0$ のとき → $k = 3$, $f = 0.5$
  • → $0.5 \times data[3] + 0.5 \times data[4]$
• $a = 3.2$ のとき → $k = 3$, $f = 0.7$
  • → $0.3 \times data[3] + 0.7 \times data[4]$
• $a = 3.4$ のとき → $k = 3$, $f = 0.9$
  • → $0.1 \times data[3] + 0.9 \times data[4]$
• $a = 3.5$ のとき → $k = 4$, $f = 0.0$
  • → $data[4]$
• $a = 3.6$ のとき → $k = 4$, $f = 0.1$
  • → $0.9 \times data[4] + 0.1 \times data[5]$
• $a = 3.8$ のとき → $k = 4$, $f = 0.3$
  • → $0.7 \times data[4] + 0.3 \times data[5]$
• $a = 4.0$ のとき → $k = 4$, $f = 0.5$
  • → $0.5 \times data[4] + 0.5 \times data[5]$

つまり、単に $a$ に近いインデックスのデータを取るだけでなく、前後のデータで重心が徐々に変化するように工夫されている様子が見えてくる。

本文中のデータ「1, 3, 5, 7, 9, 9, 14」を例に、25 パーセンタイルを実際に計算してみると $a = 7 \times 0.25 = 1.75$ で $k = 2$, $f = 0.25$ となるので、25 パーセンタイルは $0.75 \times data[2] + 0.25 \times data[3] = 0.75 \times 3 + 0.25 \times 5 = 3.50$ と計算できる。

ちなみにサイズが偶数の場合も、例えば 6 個のとき、$i = 3.0 + 0.5 = 3.5$ なので、 50 パーセンタイルは $0.5 \times data[3] + 0.5 \times data[4]$ となり、確かに中央値の定義と整合性が取れていることが確認できる。

例外処理を省いて、単純化した実装を下に示す。

def calculate_percentile(numbers, p):
    n = len(numbers)
    numbers.sort()

    # 0からインデックスが始まるように調整
    i = n * p / 100 - 0.5

    k = math.floor(i)
    f = i - k

    if f == 0:
        return data[k]
    else:
        return (1 - f) * data[k] + f * data[k + 1]

Chapter 4 のまとめ「Python からはじめる数学入門 - Chapter 4: Algebra and Symbolic Math with SymPy を読む）」を公開しました！SymPy を利用して コンピュータ代数（数式処理） の初歩を体験します。