高校数学を題材に Python の練習ができる本「Python からはじめる数学入門 (Doing Math with Python)」のまとめ。
モチベーション
今年は数学に殆ど時間を使えなかったので、来年への足がかりになり、かつ年内に気持ち良く読み切れそうな本という期待を込めて、12 月の中旬頃から原著 Doing Math with Python を読み始めた。
本の概要説明
本書は、高校数学の基本的な内容をテーマに、Python で計算をしたり可視化をする練習 ができる本と言える。日本語版のタイトルは「Python からはじめる数学入門」となっているが、あくまでも Python での取り扱いが主目的で、数学自体の解説は殆どない 事は注意が必要。
主なテーマは
- 代数学: 2 次関数など多項式関数
- 微分積分学
- ニュートン力学
- 統計学: 記述統計学
- 確率
- フラクタル
あたりで、これらの問題に対して、データ可視化用(グラフ)ライブラリ matplotlib や、コンピュータ代数(数式処理)ライブラリ SymPy などを使いながら取り組む。
よって、Python の基礎を勉強して、今後 Python で数学・数値計算などをする上での取っ掛かりが欲しい人には良い本だと思う。
環境構築
- JupyterLab を利用
- Docker Compose を利用
JupyterLab は、Python における Mathematica のノートブックみたいなもので、色々と試行錯誤しながら分析したりするのに非常に便利な環境で、デファクトスタンダードになっているようだ。使わない理由はないと思い、早速導入してみた。
また、環境のポータビリティを高めるために、これまたデファクトとなっている Docker を利用する。トップディレクトリで
$ sudo docker compose upとすれば JupyterLab が起動する。
GitHub レポジトリ https://github.com/tally1728/doing-math-with-python
各章の概略と詳細記事へのリンク
Chapter 1: Working with Numbers
四則演算から始まり、変数、数値型、ユーザ入出力、制御構文など、Python の基礎を復習する。応用としてインチとメートルなど単位の変換や、2 次方程式の数値解を計算したりする。
→ 詳細「Python からはじめる数学入門 - Chapter 1: Working with Numbers を読む」
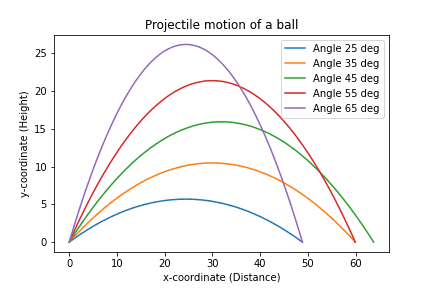
Chapter 2: Visualizing Data with Graphs
matplotlib を利用して、グラフの表示おこおなう。実例として放物運動を描いたりする。
→ 詳細「Python からはじめる数学入門 - Chapter 2: Visualizing Data with Graphs を読む」
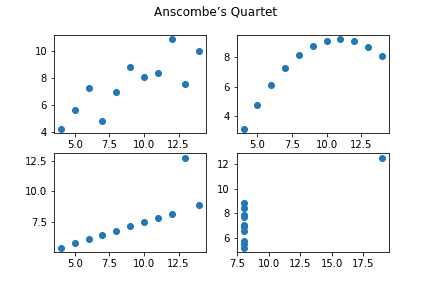
Chapter 3: Describing Data with Statistics
平均値・分散・相関係数など 記述統計学の入門編 と言える内容。それらの統計量を Python の標準ライブラリだけ用いて計算する。また matplotlib を利用して散布図を描いたりもする。
→ 詳細「Python からはじめる数学入門 - Chapter 3: Describing Data with Statistics を読む」
Chapter 4: Algebra and Symbolic Math with SymPy
コンピュータ代数(数式処理) のパッケージ SymPy を利用して、数式を展開・因数分解したり、方程式を代数的に解いたりしながら、今までの数値計算とは一味違った世界を垣間見る。
→ 詳細「Python からはじめる数学入門 - Chapter 4: Algebra and Symbolic Math with SymPy を読む」
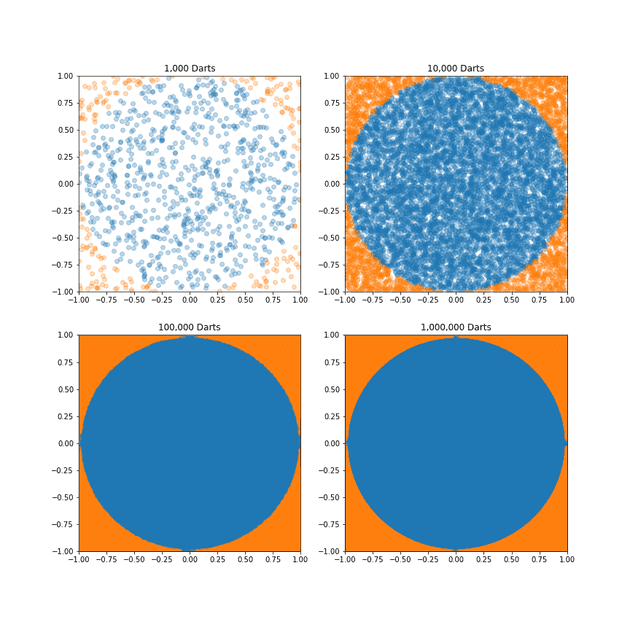
Chapter 5: Playing with Sets and Probability
本書も後半戦に入り、内容が応用的になってくる。テーマは 確率と乱数。準備として SymPy による集合を取り扱いを練習した上で、幾つか確率の計算をしてみる。乱数を用いた実験も行う。モンテカルロ法で円周率を計算したり、章末問題も面白い。
→ 詳細「Python からはじめる数学入門 - Chapter 5: Playing with Sets and Probability を読む」
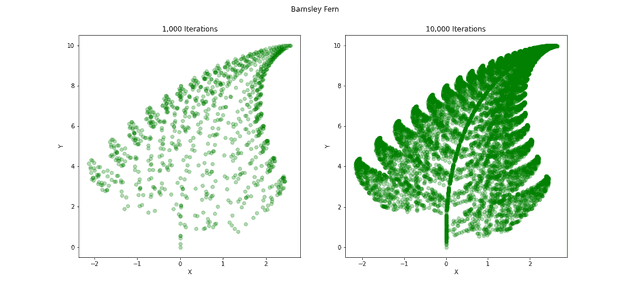
Chapter 6: Drawing Geometric Shapes and Fractals
第 2 章の続編という感じで、幾何学図形やアニメーションなど matplotlib の別の機能を試す。後半は フラクタル の摩訶不思議な世界を垣間見る。有名なマンデルブロ集合を描画したり、章末問題も好奇心をくすぐる内容で見逃せない。
→ 詳細「Python からはじめる数学入門 - Chapter 6: Drawing Geometric Shapes and Fractals を読む」
Chapter 7: Solving Calculus Problems
いよいよ最終章!第 4 章に続き、今度は 微分積分学 の初歩的な計算を SymPy で行う。SymPy の強みは数値解だけでなく、厳密解 も計算できる点にある。また応用として、関数の極値を求める 勾配降下法 を実装したりする。
→ 詳細「Python からはじめる数学入門 - Chapter 7: Solving Calculus Problems を読む」
感想
手を動かしながら、全部読み切った感想。
まず JupyterLab と SymPy と matplotlib の組み合わせは便利だと思った。SymPy は数値計算だけなく、計算機代数(数式処理)が扱えるのが良い。また SymPy は Python ベースなので、関数の引数がブラケット になったりする Mathematica よりも、違和感なく自然に使える点も非常に好印象。
数学のレベルは全然高くなくて、話題も広く浅く、若干脈略も無い印象だけど、入門書だからこんなものかな。そのかわり、よく知らなかったフラクタルなどに触れあえたのは良い経験だった。
残念だったのは、途中の 記事 でも述べたが、本文ではいたるところでリストの append() メソッドを多用して手続き型のコードを書いている点。Python で書くなら、しかもテーマが数学ならば、内包表記を利用しないのはもったいないと思う。そう思っていたら、終盤の付録で解説されていた。いつか改訂版で改善される事を願う。
とにかく Python で数学する良い地ならしにはなったと思う。数式処理・数値計算・可視化という基本要素がそろったので、自分でリファレンスを調べながら色々な計算ができる気がしてきた。
新年は、いよいよ 加藤 公一: 機械学習のエッセンス (SB クリエイティブ, 2018) を読んでみよう。